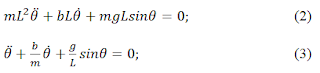A simple harmonic oscillator is a linear oscillator which is governed by the following linear characteristics equation:
A pendulum is a non-linear system due to presence of sine term in its characteristics equation. It exhibits harmonic motion only for small angle oscillations.
For small values of θ, sinθ = θ. Thus the non-linear equation becomes
Let us put the above equations in ordinary differential equation form.
The position of Pendulum bob can be found out using simple trigonometric equations:
We will use above sets of equation to write our code and simulate the behavior of a simple harmonic oscillator and a non-linear pendulum.
Symbols used:
m= mass of the pendulum (neglecting mass of the hanging string)
L= Length of the string
b = damping coefficient
g = acceleration due to gravity = 9.81 m/s2
θ = angle subtended by the string with vertical position
LabVIEW implementation
Small initial angle; x1(0) = 25⁰
The response of both linear (simple harmonic oscillator) and non-linear (Pendulum) system overlaps and identical. It holds true because for small θ, sinθ = θ. Thus equation (5) and (6) become same.
For large value of initial angle x1(0), the response of Linear and Non-linear pendulum varies as they have different angular displacements.
The “Damping enable” button allows us to enable or disable damping in our simulation.
Block Diagram of code